CS Study Fun – Khoa học máy tính

Learn & Enjoy …

«
»

Bài toán nhân đa thức – Phép biến đổi Fourier nhanh (Fast Fourier Transform) – FFT

Posted by Trần Quốc Long trên Tháng Một 12, 2009

Bài toán nhân đa thức: Cho 2 đa thức \displaystyle A(x)=a_0+a_1x+\ldots+a_{n-1}x^{n-1} và \displaystyle B(x)=b_0+b_1x+\ldots+b_{n-1}x^{n-1}, tính đa thức \displaystyle C(x) = A(x)B(x). Nghĩa là tìm các hệ số \displaystyle c_0, c_1, \ldots, c_{2n-2} của đa thức \displaystyle C(x) (Do \displaystyle A, B  có bậc \displaystyle n-1 nên \displaystyle C(x) có bậc lớn nhất là \displaystyle 2n-2).

Công thức của các hệ số \displaystyle c_k là

\displaystyle c_k = \sum_{i=0}^k a_ib_{k-i}, \forall i=0,1,\ldots,2n-2

trong đó nếu \displaystyle i\geq n ta đặt \displaystyle a_i=b_i=0. Như vậy, để tính tất cả các hệ số của đa thức \displaystyle C(x) bằng công thức trên ta cần \displaystyle O(n^2) phép tính. Tuy nhiên, ta có thể tính các hệ số của đa thức \displaystyle C(x) chỉ với độ phức tạp \displaystyle O(n\log n) bằng phép biến đổi Fourier nhanh (Fast Fourier Transform – FFT).

Một số ý tưởng dẫn đến thuật toán FFT:

  1. Một đa thức bậc nhỏ hơn \displaystyle n hoàn toàn xác định nếu ta biết giá trị của đa thức tại \displaystyle n điểm phân biệt. Tức là nếu biết \displaystyle A(x_0), A(x_1),\ldots,A(x_{n-1}) thì sẽ tính được \displaystyle a_0, a_1,\ldots,a_{n-1} và ngược lại.
  2. Như vậy, nếu ta tính được giá trị của đa thức \displaystyle A,B tại các điểm \displaystyle x_0,x_1,\ldots,x_{2n-2} thì do ta dễ dàng tính được \displaystyle C(x_i)=A(x_i)B(x_i), i=0,1,\ldots,2n-2, nên đa thức \displaystyle C(x) và các hệ số của nó hoàn toàn xác định được.
  3. Giả sử \displaystyle n chẵn và đa thức \displaystyle A(x)=a_0+a_1x+\ldots+a_{n-1}x^{n-1}, xét 2 đa thức sau

    \displaystyle A_e(x)=a_0+a_2x+a_4x^2+\ldots+a_{n-2}x^{(n-2)/2} sử dụng các hệ số bậc chẵn của \displaystyle A(x)
    \displaystyle A_o(x)=a_1+a_3x+a_5x^2+\ldots+a_{n-1}x^{(n-2)/2} sử dụng các hệ số bậc lẻ của \displaystyle A(x)

    ta thấy \displaystyle A(x)=A_e(x^2)+xA_o(x^2). Do đó nếu ta chọn tập các điểm \displaystyle x_0,x_1,\ldots x_{n-1} sao cho

    \displaystyle x_i = -x_{i+n/2},\forall i=0,1,\ldots,n/2-1
    \displaystyle x_0,x_1,\ldots,x_{n/2-1},-x_0,-x_1,\ldots, -x_{n/2-1}

    thì việc tính giá trị của đa thức \displaystyle A(x) tại \displaystyle n điểm \displaystyle x_0,\ldots,x_{n-1} được quy về tính giá trị 2 đa thức \displaystyle A_e(x), A_o(x) (có bậc nhỏ hơn \displaystyle n/2) tại \displaystyle n/2 điểm \displaystyle x_0^2, x_1^2,\ldots,x_{n/2-1}^2.

  4. Nếu tại \displaystyle n/2 điểm mới ta vẫn có tính chất một nửa số điểm trái dấu với nửa số điểm còn lại thì ta có thể tiếp tục đệ quy. Như vậy, độ phức tạp để tính toán giá trị đa thức tại \displaystyle n điểm có công thức

    \displaystyle T(n)=2T(n/2)+O(n)

    trong đó \displaystyle 2T(n/2) là độ phức tạp của 2 bài toán con, còn \displaystyle O(n) là độ phức tạp khi ta sử dụng công thức \displaystyle A(x)=A_e(x^2)+xA_o(x^2) để kết hợp kết quả của 2 bài toán con. Theo định lý tổng quát, ta có \displaystyle T(n)=\Theta(n\log n) giống trường hợp thuật toán sắp xếp trộn (Merge Sort).

  5. Tuy nhiên, để trong \displaystyle n/2 điểm \displaystyle x_0^2, x_1^2,\ldots,x_{n/2-1}^2 có một nửa số điểm trái dấu với nửa số điểm còn lại, các điểm \displaystyle x_i không thể là số thực vì \displaystyle x^2\geq 0,\forall x\in R. Như vậy, ta phải sử dụng số phức.
  6. Để ý rằng, ở trường hợp cơ sở, \displaystyle n=1, nếu ta luôn chọn \displaystyle x_0=1 để tính giá trị đa thức thì:Ở bước đệ quy trước đó, ta có các điểm \displaystyle x = \pm\sqrt{1} = \pm 1
    Ở bước đệ quy trước đó, ta có các điểm \displaystyle x = \pm\sqrt{1},\pm\sqrt{-1} = 1,-1,+i,-i
    ……
    Ở bước đệ quy với đa thức bậc nhỏ hơn \displaystyle n ta có các điểm là căn phức bậc \displaystyle n của 1 (n-th complex roots of unity).

Căn phức bậc \displaystyle n của 1:

Từ công thức nổi tiếng của Euler \displaystyle e^{i\pi}+1=0, ta có

\displaystyle e^{2i\pi}=1 \Rightarrow e^{2i\pi k}=1,\forall k=0,1\ldots, n-1

\displaystyle \Rightarrow \left(e^{2i\pi k/n}\right)^n = 1

Nghĩa là \displaystyle \omega_{k,n}=e^{2i\pi k/n}, k=0,1\ldots, n-1 là \displaystyle n căn phức bậc \displaystyle n của \displaystyle 1 .

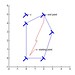
Hình sau cho thấy vị trí các căn phức của \displaystyle 1 trên đường tròn đơn vị.

Căn phức b�c 4, 5, 6 của 1

Căn phức bậc 4, 5, 6 của 1

Bây giờ ta xem xét các tính chất của căn phức bậc \displaystyle n của 1.

Tính chất 1: Nếu\displaystyle n chẵn thì \displaystyle \omega_{k,n} = -\omega_{k+n/2,n},\forall k=0,1,\ldots,n/2-1, nghĩa là tập các căn phức bậc \displaystyle n của  \displaystyle 1 chia thành 2 tập trái dấu nhau.

Chứng minh:

\displaystyle \omega_{k+n/2,n}=e^{2i\pi (k+n/2)/n} = e^{i(2\pi k/n+\pi)}
\displaystyle =\cos(2\pi k/n+\pi)+i\sin(2\pi k/n+\pi)=-\cos(2\pi k/n)-i\sin(2\pi k/n)
\displaystyle =-e^{2i\pi k/n}=-\omega_{k,n}.

Tính chất 2: Nếu\displaystyle n chẵn thì \displaystyle \omega_{k,n}^2 = \omega_{k,n/2}.

Chứng minh:

\displaystyle \omega_{k,n}^2=e^{(2i\pi k/n)2}\displaystyle =e^{2i\pi k/(n/2)}=\omega_{k,n/2}

Tính chất 3: Nếu \displaystyle z là căn phức bậc \displaystyle n của 1 thì \displaystyle \sum_{k=0}^{n-1}z^k=\begin{cases}n & z = 1\\ {0} & z\neq 1\end{cases}

Chứng minh:

\displaystyle 0=z^n-1 = (z-1)\sum_{k=0}^{n-1}z^k\displaystyle \Rightarrow z=1 hoặc \displaystyle \sum_{k=0}^{n-1}z^k=0
Với \displaystyle z=1 ta có \displaystyle \sum_{k=0}^{n-1}z^k=n.

Nhận xét: Với các tính chất 1 và 2 ở trên, nếu \displaystyle n là lũy thừa của \displaystyle 2, và nếu ta chọn tập điểm để tính giá trị của đa thức \displaystyle A(x) tại căn phức bậc \displaystyle n thì ta có thể cài đặt thuật toán đệ quy như mô tả ở phần trên. Thuật toán này được gọi là phép biến đổi Fourier nhanh (FFT hay dFFT – chữ d là discrete – rời rạc).

Vậy để tính giá trị đa thức bậc \displaystyle n tại các căn phức bậc \displaystyle n của 1 (giả sử \displaystyle n là lũy thừa của 2) ta có thuật toán FFT như sau:

procedure \displaystyle FFT(A, n)

Input: \displaystyle a_0, a_1, \ldots, a_{n-1} là các hệ số của \displaystyle A(x), trong đó \displaystyle n là lũy thừa của 2 (nếu \displaystyle n  chưa phải là lũy thừa của 2, ta chỉ cần thêm các số \displaystyle {0} vào cho đủ)

Output: giá trị của đa thức \displaystyle A(x) tại các căn phức bậc \displaystyle n của \displaystyle 1:
\displaystyle A(\omega_{0,n}),A(\omega_{1,n}),\ldots,A(\omega_{n-1,n})

  1. If  \displaystyle n=1, return \displaystyle A(\omega_{0,1})=A(1)=a_0
  2. Else Tạo 2 đa thức
    \displaystyle A_e(x)=a_0+a_2x+a_4x^2+\ldots+a_{n-2}x^{(n-2)/2}
    \displaystyle A_o(x)=a_1+a_3x+a_5x^2+\ldots+a_{n-1}x^{(n-2)/2}
  3. Call \displaystyle FFT(A_e,n/2),  \displaystyle FFT(A_o,n/2) để tính giá trị của \displaystyle A_e(x), A_0(x) tại
    \displaystyle \omega_{k,n/2}=\omega_{k,n}^2=\omega_{k+n/2,n}^2,\forall k=0,1,\ldots,n/2-1
  4. For \displaystyle k=0\rightarrow n/2-1
    \displaystyle A(\omega_{k,n}) = A_e(\omega_{k,n/2})+\omega_{k,n}A_o(\omega_{k,n/2})
    \displaystyle A(\omega_{k+n/2,n}) = A_e(\omega_{k,n/2})-\omega_{k,n}A_o(\omega_{k,n/2})

Với thuật toán FFT trong tay, ta có thuật toán nhân đa thức sau:

procedure \displaystyle PolyMult(A, B)

Input: \displaystyle a_0, a_1, \ldots, a_{n-1} là các hệ số của \displaystyle A(x),  \displaystyle b_0, b_1, \ldots, b_{n-1} là các hệ số của \displaystyle B(x). Ta cũng giả sử \displaystyle n là lũy thừa của 2.

Output: \displaystyle c_0, c_1, \ldots, c_{2n-2} là các hệ số của \displaystyle C(x)=A(x)B(x)

  1. Call \displaystyle FFT(A,2n),  \displaystyle FFT(B,2n) để tính giá trị  đa thức \displaystyle A, B tại \displaystyle \omega_{k,2n}, \forall k=0,1,\ldots,2n-1
  2. For \displaystyle k=0\rightarrow 2n-1:\displaystyle C(\omega_{k,2n}) = A(\omega_{k,2n})B(\omega_{k,2n})
  3. Lập đa thức \displaystyle D(x) với các hệ số \displaystyle d_k = C(\omega_{k,2n}), k=0,1,\ldots, 2n-1
  4. Call \displaystyle FFT(D,2n)
  5. For \displaystyle k=0\rightarrow 2n-1:\displaystyle c_k = \frac{D(\omega_{2n-k,2n})}{2n}
    trong đó \displaystyle \omega_{2n,2n}=\omega_{0,2n}=1

Để thấy thuật toán trên cho ta hệ số \displaystyle c_k,k=0,1,\ldots,2n-1 đúng, ta có định lý sau

Định lý: Với mọi \displaystyle k=0,1,\ldots,2n-1, ta có đẳng thức

\displaystyle c_k = \frac{D(\omega_{2n-k,2n})}{2n}

công thức này còn gọi là phép biến đổi Fourier ngược (inverse FFT).

Chứng minh: Thật vậy, khai triển \displaystyle D(\omega_{2n-k,2n}) ta được:

\displaystyle D(\omega_{2n-k,2n}) = \sum_{s=0}^{2n-1} d_s \omega_{2n-k,2n}^s
\displaystyle = \sum_{s=0}^{2n-1} C(\omega_{s,2n}) \omega_{2n-k,2n}^s
\displaystyle = \sum_{s=0}^{2n-1} \sum_{t=0}^{2n-1} c_t \omega_{s,2n}^t\omega_{2n-k,2n}^s
\displaystyle = \sum_{t=0}^{2n-1} c_t \sum_{s=0}^{2n-1} \omega_{s,2n}^t\omega_{2n-k,2n}^s
\displaystyle =\sum_{t=0}^{2n-1} c_t \sum_{s=0}^{2n-1} \omega_{2n-k+t,2n}^s

Theo tính chất 3 ở trên, ta có

\displaystyle \sum_{s=0}^{2n-1} \omega_{2n-k+t,2n}^s = \begin{cases}2n & \omega_{2n-k+t,2n}=1 \Leftrightarrow t=k\\ {0} & \omega_{2n-k+t,2n} \neq 1\end{cases}

Vậy \displaystyle D(\omega_{2n-k,2n}) = (2n) c_k, điều phải chứng minh.

Nhận xét:

  1. Định lý cho thấy quan hệ của các hệ số \displaystyle c_0, \ldots, c_{2n-1} và giá trị của đa thức tại căn phức của 1: \displaystyle C(\omega_{0,2n}),\ldots,C(\omega_{2n-1,2n}) qua phép biến đổi Fourier (xuôi và ngược).
    \displaystyle C_k = C(\omega_{k,n}) = \sum_{t=0}^{n-1}c_t \omega_{k,n}^t=\sum_{t=0}^{n-1}c_t e^{2i\pi kt/n}
    \displaystyle c_k = \frac{1}{n}\sum_{t=0}^{n-1}C_t e^{-2i\pi kt/n}
  2. Phép biến đổi Fourier nhanh với độ phức tạp \displaystyle O(n\log n) là công cụ tính toán quan trọng trong ngành xử lý tín hiệu số (Digital Signal Processing), hầu hết các phần mềm xử lý hình ảnh, âm thanh đều có cài đặt thuật toán FFT.
  3. Thuật toán FFT được đưa ra bởi Cooley và Tukey năm 1965, nhưng thật ra, thuật toán này đã được Gauss nghĩ ra từ năm 1805, tuy vào thời điểm đó, ông không quan tâm đến độ phức tạp thuật toán.

This entry was posted on Tháng Một 12, 2009 lúc 11:00 chiều and is filed under Chia để trị, Thuật toán. Thẻ: , , , , , , , . You can follow any responses to this entry through the RSS 2.0 feed. You can skip to the end and leave a response. Pinging is currently not allowed.

Bình luận về bài viết này

«
»