CS Study Fun – Khoa học máy tính

Learn & Enjoy …

«
»

Thuật toán giãn affine (1) – Ý tưởng thiết kế và thuật toán

Posted by Trần Quốc Long trên Tháng Ba 1, 2008

Thuật toán giãn affine (affine scaling algorithm) là một trong các thuật toán điểm trong giải bài toán QHTT. Ý tưởng chính của các phương pháp này là xuất phát từ một nghiệm bên trong đa diện lồi, ta lần lượt tìm các nghiệm khác có giá trị hàm mục tiêu tốt hơn và đi dần tới nghiệm tối ưu (có thể nghiệm này ở trên biên).

Ý tưởng thiết kế: Do rất khó đưa ra lời giải tối ưu của bài toán QHTT dưới dạng công thức (nếu có, công thức này sẽ phải tính từ \displaystyle A,b,c), tại mỗi bước lặp, người ta bao nghiệm đang xét\displaystyle x>0 bằng một hình ellipse trong\displaystyle E\subset\mathbb{R}^n. Hình ellipse này được chọn sao cho các điểm \displaystyle y\in E vẫn thỏa mãn \displaystyle y>0, đồng thời bài toán QHTT giới hạn trong hình ellipse này có lời giải \displaystyle x^* dưới dạng công thức (phụ thuộc vào \displaystyle A,b,c và công thức của \displaystyle E). Sau đó ta lại bao \displaystyle x^* bằng một hình ellipse khác và cứ tiếp tục như vậy đến khi khoảng cách đối ngẫu nhỏ hơn một ngưỡng \displaystyle \epsilon>0 nào đó.

Code trong Matlab của thuật toán giãn affine, cùng với code chạy thuật toán trên ví dụ ta đã xét ở loạt bài về Phương pháp đơn hình, download ở đây :-)

\displaystyle \min~ -x_1-x_2
\displaystyle \begin{array}{rrr}-x_1&+2x_2&\leq 8\\2x_1&+x_2&\leq 9\\3x_1&-x_2&\leq 6\\x_1,x_2&&\geq 0\end{array}

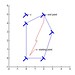
Quá trình chạy thuật toán giãn affine trong ví dụ trên

Bây giờ ta xét chi tiết từng bước của thuật toán:

Định lý (hình ellipse dương bao lấy một điểm): Giả sử \displaystyle x>0 thuộc \displaystyle \mathbb{R}^n và \displaystyle 0<\beta<1 . Khi đó tập

\displaystyle E(x) = \left\{y\in \mathbb{R}^n:\sum_{i=1}^n \frac{(y_i-x_i)^2}{x_i^2}=||X^{-1}(y-x)||^2\leq \beta^2 \right\}

là ellipse trong \displaystyle \mathbb{R}^n mà \displaystyle y>0,\forall y\in E(x). Trong đó\displaystyle X=\mathrm{diag}(x_1,\ldots,x_n) là ma trận đường chéo tạo bởi véctơ\displaystyle x.

Chứng minh: Dễ thấy

\displaystyle y\in E(x) \Rightarrow \frac{(y_i-x_i)^2}{x_i^2}\leq \beta^2,\forall i

\displaystyle \Rightarrow |y_i-x_i|\leq \beta x_i<x_i,\forall i

do \displaystyle x_i>0,0<\beta<1. Suy ra \displaystyle y_i>0,\forall i.

Quay lại bài toán QHTT dạng chuẩn tắc

\displaystyle \min c^Tx, x\in P=\{Ax=b,x\geq 0\}

Bây giờ ta bao \displaystyle x bằng hình ellipse \displaystyle E(x) và tìm điểm \displaystyle x^*\in E(x)\cap P sao cho \displaystyle c^Tx^*\leq c^Ty,\forall y\in E(x)\cap P. Tức là ta phải tìm nghiệm tối ưu của bài toán

\displaystyle \min \{c^Ty:Ay=b,||X^{-1}(y-x)||^2\leq \beta^2,y\geq 0\}

Lưu ý, ta có thể bỏ ràng buộc \displaystyle y\geq 0 do\displaystyle y>0,\forall y\in E(x).

Nếu ta đổi biến \displaystyle d=y-x thì ta có bài toán tương đương

\displaystyle \min \{c^Td:Ad=0,||X^{-1}d||^2\leq \beta^2\}

Có thể hiểu đây là bài toán tìm hướng tốt nhất để biến đổi \displaystyle x thành nghiệm tối ưu \displaystyle x^*\in E(x)\cap P.

Đây là bài toán quy hoạch lồi, hàm Lagrange tương ứng là

\displaystyle L(d,\mu,\lambda)=c^Td+\mu (||X^{-1}d||^2-\beta^2)-\lambda^TAd

Ta có thể viết điều kiện Karush-Kuhn-Tucker (KKT) cho nghiệm tối ưu \displaystyle d^* của bài toán này như sau:

\displaystyle \exists \mu\geq 0,\lambda:\begin{cases}\nabla_d L(d^*,\mu,\lambda)=\nabla_d\{c^Td^*+\mu (||X^{-1}d^*||^2-\beta^2)-\lambda^TAd^*\}=0\\ \mu(||X^{-1}d^*||^2-\beta^2)=0\end{cases}

Giải hệ này ta được

\displaystyle \lambda=(AX^2A^T)^{-1}AX^2c

\displaystyle \mu=\frac{||X(c-A^T\lambda)||}{2\beta}

\displaystyle d^*=\frac{X^2(A^T\lambda-c)}{2\mu}=-\beta\frac{X^2(c-A^T\lambda)}{||X(c-A^T\lambda)||}

Để thấy \displaystyle d^* là nghiệm tối ưu, ta có

\displaystyle Ad^*=\frac{AX^2(A^T\lambda-c)}{2\mu}=\frac{AX^2A^T\lambda-AX^2c}{2\mu} = 0

\displaystyle ||X^{-1}d^*||=|-\beta|\frac{||X(c-A^T\lambda)||}{||X(c-A^T\lambda)||}=\beta

Hơn nữa nếu xét một nghiệm \displaystyle d bất kì của bài toán, do \displaystyle Ad=0,||X^{-1}d||\leq \beta ta có

\displaystyle c^Td = (c^T-\lambda^TA)d=(c^T-\lambda^TA)XX^{-1}d

\displaystyle \geq -||X(c-A^T\lambda)||.||X^{-1}d||\geq -\beta||X(c-A^T\lambda)||

trong khi đó

\displaystyle c^Td^*=-(c^T-\lambda^TA)\beta\frac{X^2(c-A^T\lambda)}{||X(c-A^T\lambda)||}

\displaystyle =-\beta||X(c-A^T\lambda)||\leq c^Td

Như vậy \displaystyle d^* là nghiệm tối ưu. Ta tổng kết lại bằng định lý sau:

Định lý (hướng tốt nhất trong hình ellipse): Nếu \displaystyle x>0 là một điểm nằm trong đa diện lồi dạng chuẩn tắc\displaystyle P=\{Ax=b,x\geq 0\} và \displaystyle 0<\beta<1 , đồng thời các hàng của \displaystyle A độc lập tuyến tính và \displaystyle c không phải là tổ hợp tuyến tính các hàng của \displaystyle A, đặt

\displaystyle d^*=\frac{X^2(A^T\lambda-c)}{2\mu}=-\beta\frac{X^2(c-A^T\lambda)}{||X(c-A^T\lambda)||}

với \displaystyle \lambda=(AX^2A^T)^{-1}AX^2c. Khi đó \displaystyle d^* là hướng tốt nhất sao cho \displaystyle x^*=x+d^* là nghiệm tối ưu trong tập\displaystyle E(x)\cap P.

Nhận xét:

  1. Ta phải đưa thêm các điều kiện “các hàng của \displaystyle A độc lập tuyến tính” và “\displaystyle c không phải tổ hợp tuyến tính các hành của \displaystyle A” để ma trận\displaystyle AX^2A^T khả nghịch và véctơ \displaystyle c-A^T\lambda\neq 0.
  2. Nếu các hàng của \displaystyle A không độc lập tuyến tính, ta có thể loại đi một số hàng phụ thuộc tuyến tính vào các hàng khác.
  3. Nếu\displaystyle c=A^T\alpha thì\displaystyle \lambda=(AX^2A^T)^{-1}AX^2c=(AX^2A^T)^{-1}AX^2A^T\alpha=\alpha, suy ra \displaystyle c-A^T\lambda=A^T\alpha-A^T\alpha=0. Hơn nữa\displaystyle c^Tx=\alpha^TAx=\alpha^Tb không phụ thuộc vào \displaystyle x, nghĩa là mọi nghiệm chấp nhận được đều là nghiệm tối ưu.
  4. Nếu\displaystyle x là một nghiệm cơ sở chấp nhận được \displaystyle x=(x_1,\ldots,x_m,0,\ldots,0), \displaystyle X=\mathrm{diag}(x_1,\ldots,x_m,0,\ldots,0) và \displaystyle A=\left[\begin{array}{cc}B&N\end{array}\right] ta có \displaystyle AX=\left[\begin{array}{cc}BX&0\end{array}\right] và
    \displaystyle \lambda = (AX^2A^T)^{-1}AX^2c
    \displaystyle =(B^T)^{-1}X_0^{-2}B^{-1}BX_0^2c_B=(B^T)^{-1}c_B

    trong đó\displaystyle X_0=\mathrm{diag}(x_1,\ldots,x_m). Nghĩa là \displaystyle \lambda chính là nghiệm cơ sở đối ngẫu của\displaystyle x. Trong trường hợp \displaystyle x không phải là nghiệm cơ sở chấp nhận được ta gọi \displaystyle \lambda là ước lượng đối ngẫu của \displaystyle x. Hơn nữa, véctơ \displaystyle \bar{c}^T=c^T-c_B^TB^{-1}A=c^T-\lambda^TA chính là véctơ chứa giá trị thay đổi ở các hướng trong thuật toán đơn hình.

  5. Nếu \displaystyle x là nghiệm cơ sở bị suy biến, ma trận \displaystyle AX^2A^T không khả nghịch, do đó ta giả sử mọi nghiệm cơ sở đều không suy biến.
  6. Nếu \displaystyle d^*\geq 0 hay\displaystyle -X^2\bar{c}\geq 0 thì bài toán không bị chặn và không có nghiệm tối ưu.
  7. Hướng \displaystyle d_{\mathrm{max}}=-d^* là hướng cực đại hóa hàm mục tiêu (vì hệ phương trình của điều kiện KKT thật ra có 2 nghiệm \displaystyle d^*,-d^*).
  8. Nếu\displaystyle \bar{c}=c-A^T\lambda\geq 0, ta có \displaystyle \lambda là nghiệm chấp nhận được của bài toán đối ngẫu, khi đó khoảng cách đối ngẫu (duality gap) là
    \displaystyle c^Tx-\lambda^Tb=c^Tx-\lambda^TAx=\bar{c}^Tx

Định lý (khoảng cách đối ngẫu): Nếu \displaystyle x và \displaystyle \lambda là hai nghiệm chấp nhận được của bài toán gốc \displaystyle (P) và bài toán đối ngẫu \displaystyle (D) và khoảng cách đối ngẫu

\displaystyle c^Tx-\lambda^Tb<\epsilon

thì

\displaystyle \mathrm{Opt}(P)\leq c^Tx<\mathrm{Opt}(P)+\epsilon

\displaystyle \mathrm{Opt}(D)\geq \lambda^Tb>\mathrm{Opt}(P)-\epsilon

trong đó \displaystyle \mathrm{Opt}(P),\mathrm{Opt}(D) là giá trị tối ưu của hai bài toán.

Chứng minh: Theo định lý về tính đối ngẫu của hai bài toán, ta có

\displaystyle \lambda^Tb\leq \mathrm{Opt}(D)=\mathrm{Opt}(P).

Suy ra \displaystyle \displaystyle \epsilon>c^Tx-\lambda^Tb\geq c^Tx-\mathrm{Opt}(P) hay

\displaystyle c^Tx<\mathrm{Opt}(P)+\epsilon

Chứng minh tương tự cho \displaystyle \lambda.

Nhận xét: Định lý cho ta điều kiện để kiểm tra một nghiệm có gần với nghiệm tối ưu hay không bằng cách kiểm tra khoảng cách đối ngẫu.

Tổng kết lại, ta có thuật toán giãn affine sau

Đầu vào (input):

  • Các ràng buộc và hàm mục tiêu \displaystyle A,b,c.
  • Một nghiệm chấp nhận được \displaystyle x>0.
  • Ngưỡng kiểm tra điều kiện tối ưu\displaystyle \epsilon>0.
  • Tham số \displaystyle 0<\beta<1.

Thuật toán giãn affine:

  1. Tính các đại lượng
    \displaystyle X=\mathrm{diag}(x_1,\ldots,x_n)
    \displaystyle \lambda=(AX^2A^T)^{-1}AX^2c
    \displaystyle \bar{c}=c-A^T\lambda.
  2. Kiểm tra điều kiện tối ưu: Nếu\displaystyle \bar{c}\geq 0 và \displaystyle \bar{c}^Tx<\epsilon thì dừng và đưa ra nghiệm\displaystyle x.
  3. Nếu \displaystyle -X^2\bar{c}\geq 0 thì dừng và kết luận bài toán không bị chặn và không có nghiệm.
  4. Cập nhật nghiệm
    \displaystyle x\leftarrow x+d^*=x-\beta\frac{X^2\bar{c}}{||X\bar{c}||}

    và quay lại bước 1.

Nhận xét:

  1. Sau mỗi vòng lặp, giá trị hàm mục tiêu thay đổi một lượng bằng
    \displaystyle c^Td^*=(c^T-\lambda^TA)d^*=-\beta||X(c-A^T\lambda)||=-\beta||X\bar{c}||<0
  2. Ta có thể viết
    \displaystyle d^*=-\beta X\frac{X\bar{c}}{||X\bar{c}||}=-\beta Xh
    \displaystyle =-\beta \left[\begin{array}{ccc}x_1h_1&\ldots&x_nh_n\end{array}\right]^T

    với \displaystyle ||h||=1. Như vậy \displaystyle ||d^*||_1\leq \beta||x||, với \displaystyle ||.||_1 là chuẩn \displaystyle L_1, tức là khi \displaystyle x\rightarrow 0 (\displaystyle x tiến đến một điểm cực biên) thì \displaystyle ||d^*||\rightarrow 0, tức là thay đổi của \displaystyle x^* so với \displaystyle x sẽ không lớn. Có thể hiểu là khi \displaystyle x gần chạm đến biên thì bán kính của hình ellipse \displaystyle E(x) nằm gọn trong \displaystyle P sẽ không lớn, nên \displaystyle ||d^*|| nhỏ.

  3. Trong thực hành, người ta thấy khi \displaystyle x gần đến biên thì thuật toán sẽ biến đổi\displaystyle x chạy dọc theo biên của đa diện lồi (gần giống với phương pháp đơn hình). Vì vậy, người ta tin là độ phức tạp của thuật toán affine cũng giống với độ phức tạp của thuật toán đơn hình (mặc dù chưa có chứng minh).
  4. Đây cũng là xuất phát điểm của các phương pháp điểm trong khác, các phương pháp này ngoài việc làm giảm giá trị hàm mục tiêu còn luôn giữ \displaystyle x cách xa biên của đa diện lồi, đảm bảo thay đổi \displaystyle d^* đủ lớn. Các phương pháp này được chứng minh là có thời gian đa thức phụ thuộc vào số biến \displaystyle n, số ràng buộc \displaystyle m và số bít để mô tả độ chính xác của nghiệm\displaystyle \ln \frac{1}{\epsilon} (để ý rằng \displaystyle \epsilon là độ chính xác của nghiệm).
  5. Làm thế nào để khởi tạo nghiệm \displaystyle x>0, ta có thể thêm vào một biến \displaystyle x_{n+1} và giải bài toán QHTT sau
    \displaystyle \min \{c^Tx+Mx_{n+1}: Ax + (b-Ae)x_{n+1}=b,(x,x_{n+1})\geq 0\}

    trong đó \displaystyle e>0 bất kì còn \displaystyle M là một số rất lớn so với các giá trị trong \displaystyle c. Khi đó \displaystyle (x,x_{n+1})=(e,1)>0 là nghiệm chấp nhận được ban đầu để ta khởi tạo thuật toán giãn affine. Để ý rằng, nếu bài toán gốc có nghiệm tối ưu \displaystyle x^* thì \displaystyle (x^*,0) là nghiệm tối ưu của bài toán trên do \displaystyle M là số rất lớn.

This entry was posted on Tháng Ba 1, 2008 lúc 1:40 chiều and is filed under Quy hoạch tuyến tính. Thẻ: , , , , , , , , , , . You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, hoặc trackback from your own site.

Bình luận về bài viết này

«
»